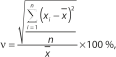Управление запасами

Одним из ключевых элементов оптимизации цепей поставок является процесс управления запасами в рамках всей цепи поставок. Создание интегрированной системы управления запасами позволит минимизировать общие активы цепи, связанные с запасами.

Высокие уровни запасов на протяжении всей цепи поставок являются симптомом низких показателей функционирования системы. Как правило, большие объемы запасов продукции объясняются опасением возникновения дефицита, что может привести к сбоям в работе цепи поставок, а для производственных предприятий — к полной остановке производства, а это влечет за собой серьезные убытки. Чтобы избежать подобной ситуации и обеспечить высокие уровни обслуживания при низких уровнях запасов, необходимо устранить источники нестабильности и неопределенности в цепи поставок.

Классическая модель управления запасами является детерминированной моделью и предназначена для оптимизации размера текущей части запаса. В торговых организациях при управлении товарными запасами речь идет об оптимизации размера заказа (партии закупки или поставки), а в управлении товарными (сбытовыми) запасами готовой продукции предприятий-производителей — об оптимизации партий отгрузки товара.

Обратите внимание. Оптимизация размера заказа (партии поставки) означает, что необходимо найти такое его количественное значение, которое потребует минимальных затрат на формирование и содержание текущего запаса при заданных условиях.

Методика решения данной задачи базируется на том, что различные составляющие затрат изменяются разнонаправлено при изменении размера партии поставки. Следовательно, существует такой размер партии закупки, который обеспечивает минимум общих (суммарных) затрат, связанных с формированием и содержанием запаса. Наименьшие затраты будут определять оптимальную стратегию закупки материального ресурса в заданных условиях, то есть минимум удельных затрат является критерием оптимальности выбора размера заказа (объема партии поставки) и максимального уровня текущего запаса.

Классическая экономико-математическая модель запасов имеет следующий вид:

h / Q = 2 × k × b,

где h — стоимость содержания единицы запасов в единицу времени;

Q — оптимальный размер партии поставки;

k — условно-постоянные затраты, связанные с закупкой и поставкой одной партии;

b — среднесуточный расход (продажа) материального ресурса.

Эту модель теории управления запасами называют формулой Уилсона (Вилсона) по имени ее автора (R. H. Wilson).

Проведем разделение товаров на группы с применением АВС-классификации (по доле среднегодового запаса позиции в общем объеме товарных запасов), а также XYZ-классификацию, учитывающую неравномерность спроса на различные товарные позиции. Построим совмещенную матрицу АBC-XYZ. Ассортимент товаров, среднегодовые запасы, среднеквартальные объемы продаж по каждой товарной позиции представлены в табл. 1.

Выполним АВС-классификацию с использованием табл. 2. При разбиении на группы используем следующие границы интервалов групп:

• группа А ≤ 80 %;
• 80 % < группа В ≤ 90 %;
• 90 % < группа С ≤ 100 %.

*Доля запаса по позиции в общем объеме запаса рассчитывается как средний запас по позиции × 100 / 15 625.

**Доля нарастающим итогом рассчитывается как сумма доли нарастающим итогом предыдущей позиции с долей запаса по позиции в общем объеме запаса.

Проведение XYZ-анализа выполняется с использованием табл. 3. При разбиении на группы используется классический вариант:

• группа Х < 10 %;
• 10 % ≤ группа Y < 25 %;
• группа Z ≥ 25 %.

где xi — значение спроса в i-м периоде;

 — среднее арифметическое (среднемесячное, среднеквартальное, среднегодовое) значение спроса по оцениваемому периоду;

n — количество периодов (месяцев, кварталов, лет), за которые проведена оценка.

Построение матрицы ABC-XYZ проводится по результатам выполненных ранее АВС- и XYZ-классификаций (табл. 4).

Пример 1

Рассмотрим построение модели с фиксированным размером заказа. Выполним расчеты параметров модели и представим в табл. 5 движение запаса при отсутствии задержек в поставках на 30 дней.

Исходные данные:

• расчетный период — 30 дн.;
• объем потребности — 300 ед.;
• оптимальных размер заказа — 60 ед.;
• время выполнения заказа — 3 дн.;
• время задержки поставки — 1 день;
• остаток запаса на 1-е число — 50 ед.

Страховой запас (Zs) рассчитывается по следующей формуле:

Zs = Sд × tзп,

где Sд — ожидаемое дневное потребление запаса, ед.;

tзп — время задержки поставки, дн.

Ожидаемое дневное потребление запаса (Sд) рассчитывается исходя из ожидаемой потребности в запасе за весь период:

Sд = S / N,

где S — объем потребности в запасе;

N — количество рабочих дней в плановом периоде.

Пороговый уровень запаса (ПУ):

ПУ = ОП + Zs,

ОП = Sд × tвз,

где ОП — ожидаемое потребление за время выполнения заказа, ед.;

tвз — время выполнения заказа, дн.

Максимальный желательный запас (МЖЗ):

МЖЗ = Zs + Q`,

где Q` — оптимальный размер заказа, ед.

Движение запаса приводится в табл. 6.

Пример 2

Построим модель с фиксированным интервалом времени между заказами. Для этого выполним расчеты параметров модели и представим движение запаса при отсутствии задержек в поставках.

Исходные данные:

• расчетный период — 360 дн.;
• объем потребности — 1520 ед.;
• оптимальных размер заказа — 40 ед.;
• время выполнения заказа — 3 дн.;
• время задержки поставки — 1 день;
• остаток запаса на 1-е число — 50 ед.

Первый заказ делается в первый день.

Выполним расчеты параметров модели и представим движение запаса при отсутствии задержек в поставках на 45 дней.

Расчеты параметров модели выполнены в табл. 7.

Фиксированный интервал времени между заказами (tмз, дн.) определяется на основе предварительно рассчитанного оптимального размера заказа по формуле:

tмз = N × Q` / S,

где N — количество рабочих дней в плановом периоде;

Q` — оптимальный размер заказа;

S — объем потребности в запасе.

Исходные данные для расчета параметров модели:

• объем потребности в запасе;
• интервал времени между заказами;
• время выполнения заказа;
• время задержки поставки.

Расчетные параметры:

• страховой запас; 
• максимальный желательный запас.

Через фиксированные интервалы времени требуется пополнение запаса до максимально желательного уровня (МЖЗ). Размер очередного заказа рассчитывается по формуле:

Q = МЖЗ – ZТ + ОП – Zt,

где ZT — уровень текущего запаса при выдаче заказа;

Zt — объем запаса в пути, не полученного к моменту выдачи заказа.

Движение запаса и расчет размера заказа приводится в табл. 8.

Д. И. Панферов, эксперт